논문통계방법 무료자료

윌콕슨 순위합 검정(wilcoxon rank sum test)

이 분석은 2집단 간 측정값 비교를 위한 분석입니다

보통 2집단 간 측정값 비교는 독립표본 t검정을 활용하는데요, t검정은 평균과 표준오차 값에 기반하는 만큼 표본의 정규성이 가정되어야 합니다

반면 윌콕슨 순위합 검정은 평균과 표준오차를 통해 유의성을 계산하는 것이 아니라, 표본들의 크기 순으로 나열하여 A집단 표본들의 순위, B집단 표본들의 순위만을 고려하기 때문에 정규성이 가정될 필요가 없습니다

예를 들어 아래 표와 같은 측정값을 가진 두 집단이 있다고 가정합니다

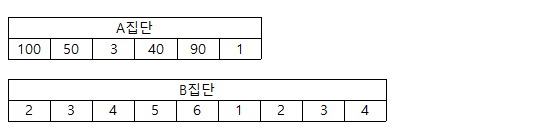
A집단의 분포는 매우 극단적이고 이를 평균으로 계산하면 41.3으로 매우 높기 때문에, B집단의 평균 3.3과 큰 차이가 있습니다

이 데이터를 t검정으로 분석하면

t=2.573, p=.050으로 유의수준 5% 기준에서 차이가 있다는 결과가 나옵니다

반면 크고 작음만을 고려한다면 A집단에도 작은 값들이 존재하기 때문에 순위합에 대단한 차이가 나타나지는 않습니다

이 데이터를 윌콕슨 검정으로 분석하면

Z=-1.601 p=.109로 유의하지 않은 결과가 나옵니다

위의 데이터는 A집단의 분포가 극단적이고 표본의 수도 적기 때문에 이러한 상반된 결과에서는 윌콕슨 검정을 더 신뢰할 수 있을 것입니다